7531. Landline Telephone Network
The mayor of RMRCity wants to create a secure landline
telephone network for emergency use in case of serious disasters when the city
is cut off from the outside world. Some pairs of buildings in the city can be
directly connected with a wire telephone line and the municipality engineers
have prepared an estimate of the cost of connecting any such pair.
The mayor needs your help to find the cheapest network that
connects all buildings in the city and satisfies a particular security measure
that will be explained shortly. A call from a building A to another building B
may be routed through any simple path in the network (i.e., a path that does
not have any repeated building). There are also some insecure buildings that
one or more persons with serious criminal records live in. The mayor wants only
communications intended for these insecure buildings to reach them. In other
words, no communication from any building A to any building B should pass
through any insecure building C in the network (where C is different from A and
B).
Input. The first line contains three
integers n, m, p where n (1 ≤ n ≤ 1000) is the number of buildings, m (0 ≤ m ≤ 105) is the number of possible direct connections between a pair
of buildings, and p (0 ≤ p ≤ n) is the number of insecure buildings. The buildings are numbered
from 1 to n. The second line contains
p distinct integers between 1 and n (inclusive), which are the numbers of
insecure buildings. Each of the next m
lines contains three integers xi,
yi and li describing one potential
direct line, where xi and yi (1 ≤ xi, yi ≤ n)
are the distinct buildings the line connects, and li (1 ≤ li
≤ 10000) is the estimate of the cost of connecting these buildings. There
is at most one direct link between any two buildings in these m lines.
Output. Display the cost of the cheapest
network satisfying the security measure if it is possible. Otherwise, print “impossible”.
|
Sample
input 1 |
Sample
output 1 |
|
4 6 1 1 1 2 1 1 3 1 1 4 1 2 3 2 2 4 4 3 4 3 |
6 |
|
|
|
|
Sample
input 2 |
Sample
output 2 |
|
4 3 2 1 2 1 2 1 2 3 7 3 4 5 |
impossible |
SOLUTION
graphs – minimal spanning
tree – Kruskal algorithm
Algorithm analysis
Find the value of
the minimum spanning
tree for all buildings except
unsafe ones. Then connect each
unsafe building to the nearest safe one. The required network cannot be
constructed if the graph is disconnected.
Separately,
analyze the case when there are no safe buildings in the city. If there is only
one unsafe building, then the answer is 0, if there are two
unsafe
buildings, then the
answer equals to the distance
between them. If there are more than 2 unsafe buildings, then the desired
network does not exist.
Example
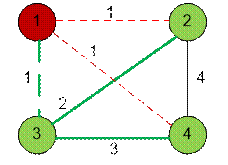
Let’s look at the first sample. The unsafe
house has number 1. Build the MST for the vertices 2, 3, 4 – its value is 5. Connect
the house number 1 to MST. The cost of the cheapest network is 6.
Let’s consider the second sample. Unsafe
house numbers are 1 and 2. Unsafe house number 1 must be directly connected to
a safe house, which is impossible for the given network. Therefore, the answer
is impossible.
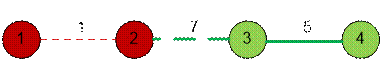
Algorithm realization
Declare the constant
infinity INF. Store the edges of the graph in the array v.
#define INF 1000000
struct Edge
{
int u,
v,dist;
Edge(int u, int v, int dist) :
u(u), v(v), dist(dist) {};
};
vector<Edge>
e;
If u is an unsafe house, then danger[u]
will store the distance from it to the nearest safe house.
vector<int> danger;
The function lt is a comparator for graph edges.
int lt(Edge a, Edge b)
{
return
(a.dist < b.dist);
}
The main part of the program. Read the input data. Initialize the
array mas for the system of disjoint sets.
scanf("%d %d %d",&n,&m,&p);
mas.resize(n +
1);
for(i = 1; i <= n; i++) mas[i] = i;
Read the unsafe houses u.
danger.resize(n
+ 1);
for(i = 0; i < p; i++)
{
scanf("%d",&u);
danger[u] = INF;
}
We are looking for the shortest distance from unsafe houses
to the nearest safe ones. Make the recalculations for such edges (u,
v), where one vertex belongs to a
safe house, and the other to an unsafe one.
for(i = 0; i < m; i++)
{
scanf("%d %d
%d",&u,&v,&dist);
if
((danger[u] > 0) && (danger[v] == 0))
danger[u] = min(danger[u],dist);
if
((danger[v] > 0) && (danger[u] == 0))
danger[v] = min(danger[v],dist);
If both vertices are safe houses, then add the corresponding
edge to the graph.
if
((danger[u] == 0) && (danger[v] == 0))
e.push_back(Edge(u,v,dist));
}
If graph does not contain edges, then the answer is 0.
if (m == 0)
{
puts("0");
return 0;
}
If graph contains one edge that connects two houses (safe or unsafe), then print
the distance between them.
if (m == 1)
{
printf("%d\n",dist);
return 0;
}
Sort the edges of the graph. The array e stores only the edges that connect the safe houses.
sort(e.begin(),e.end(),lt);
Run the Kruskal algorithm. Find the value res of MST. In the variable cnt, count the
number of edges in the constructed network.
cnt = res = 0;
for(i = 0; i < e.size(); i++)
if (Union(e[i].u,e[i].v))
{
res += e[i].dist;
cnt++;
}
Connect the
unsafe
houses to MST. Add to res the distance
from them to the nearest safe houses.
for (i = 1; i <= n; i++)
if (danger[i] > 0)
{
res += danger[i];
cnt++;
}
If the resulting graph is not connected or the size of the
resulting network is greater than infinity INF (for example, there is an unsafe
house from which there is no way to MST), then the answer is impossible.
Otherwise, print the length res of the MST.
if ((cnt != n - 1) || (res > INF))
puts("impossible");
else
printf("%d\n",res);
Java realization
import java.util.*;
class Edge
{
int u, v, dist;
Edge (int u, int v, int dist)
{
this.u = u;
this.v = v;
this.dist = dist;
}
};
public class Main
{
static int mas[];
static int size[];
static int Repr(int n)
{
while (n != mas[n]) n = mas[n];
return n;
}
static boolean Union(int x,int y)
{
x = Repr(x);
y = Repr(y);
if (x == y) return false;
mas[y] = x;
return true;
}
public static class MyFun implements
Comparator<Edge>
{
public int
compare(Edge a, Edge b)
{
return a.dist - b.dist;
}
}
public static void
main(String[] args)
{
Scanner con = new
Scanner(System.in);
int n = con.nextInt();
int m = con.nextInt();
int p = con.nextInt();
mas = new int[n+1];
for(int i = 1;
i <= n; i++)
mas[i] = i;
int danger[] = new int[n+1];
for (int i = 0;
i < p; i++)
{
int u = con.nextInt();
danger[u] = Integer.MAX_VALUE;
}
Vector<Edge> e = new
Vector<Edge>();
int dist = 0;
for(int i = 0;
i < m; i++)
{
int u = con.nextInt();
int v = con.nextInt();
dist = con.nextInt();
if ((danger[u]
> 0) && (danger[v] ==
0))
danger[u] = Math.min(danger[u], dist);
if ((danger[v]
> 0) && (danger[u] ==
0))
danger[v] = Math.min(danger[v], dist);
if ((danger[u] ==
0) && (danger[v] ==
0))
e.add(new
Edge(u, v, dist));
}
if (m ==
0)
{
System.out.println("0");
System.exit(0);
}
if (m ==
1)
{
System.out.println(dist);
System.exit(0);
}
Collections.sort(e, new MyFun());
int cnt = 0;
long res = 0;
for (int i = 0;
i < e.size(); i++)
if (Union(e.get(i).u, e.get(i).v))
{
res += e.get(i).dist;
cnt++;
}
for (int i = 1;
i <= n; i++)
if (danger[i]
> 0)
{
res += danger[i];
cnt++;
}
if ((cnt != n - 1)
|| (res > Integer.MAX_VALUE))
System.out.println("impossible");
else
System.out.println(res);
con.close();
}
}